LogP and logD calculations
This background material explains the theory behind the log P and log D calculation:
Introduction
The mass flux of a molecule at the interface of two immiscible solvents is governed by its lipophilicity. The more lipophilic a molecule is, the more soluble it is in lipophilic organic phase. For the same reason drug penetration into a biological membrane is also influenced by the lipophilicity of the drug. When a molecule is ionizable at a given pH, it forms a hydrophilic anion or cation and subsequently fails to dissolve in organic phase. Ionization of a molecule leads to the accumulation of the hydrophilic form in the aqueous phase. In contrast, its lipophilic form decreases in both aqueous and organic phase due to the law of conservation of mass.
The partition coefficient of a molecule observed in a water– n -octanol system has been adopted as the standard measure of lipophilicity. The observed partition coefficient depends on the support electrolyte concentration of the bulk phase the compound is dissolved in. Extra ion-pair forming chemical agents added to the aqueous/organic phase may have a significant effect on the partitioning behavior of a molecule.
It is often meaningful to obtain the partition coefficients of molecules by calculation. The molecular structure and extent of ionization are the primary factors in calculating the partition coefficient. The standard partition coefficient of ionized and unionized species calculated from the molecular structure is based largely on the atomic log P increments given in Viswanadhan et al.The extent of ionization at a given pH is obtained from the predicted p K a of the molecule. Our calculation method takes into account the effect of the counterion concentration on log D and log P .
Symbols used
Throughout the document we use the following symbols:
-
P i (upper case) is the macro partition coefficient, where subscript i refers to the ionization state of species included in P i, e.g. i= -2, -1, 0, +1, +2
-
p i (lower case) is the micro partition coefficient, where subscript i refers to the microspecies, e.g. i=1,2,3,4,…
-
D is the distribution coefficient
-
[ ] means concentration of microspecies
-
log P is the logarithm of the partition coefficient
Definition of logP and logD
The partition coefficient is the ratio of the concentration of the compound in octanol to its concentration in water. The distribution coefficient is the ratio of the sum of the concentrations of all species of the compound in octanol to the sum of the concentrations of all species of the compound in water. Based on acidic/basic dissociation reactions, we can introduce the concept of a partition coefficient for cationic and anionic species and for neutral species.
The following figure gives the definition of partition and distribution coefficients for ionized and unionized species.
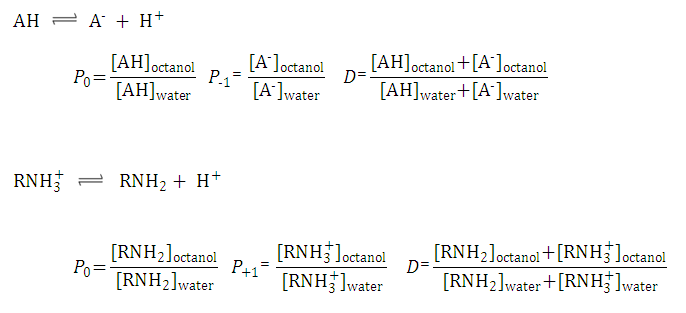 Fig. 1 Partition and distribution coefficients for ionized and unionized species
Fig. 1 Partition and distribution coefficients for ionized and unionized species
The partition and distribution coefficients for multiprotic compounds are defined in much the same way as for monoprotic compounds using the following formulae.

Fig. 2 Partition and distribution coefficients for multiprotic compounds
Example
In this example we suppose that a compound A 1A 2B 1B 2 contains two acidic and two basic ionization sites. This compound has 16 protonation states in aqueous solution. The microspecies which are assigned to the protonation states are summarized in the following table.
| Microspecies | charge |
|---|---|
| A1A2B1B2 | 0 |
| A1-A2B1B2 | -1 |
| A1A2-B1B2 | -1 |
| A1A2B1+B2 | +1 |
| A1A2B1B2+ | +1 |
| A1-A2-B1B2 | -2 |
| A1-A2B1+B2 | 0 |
| A1-A2B1B2+ | 0 |
| A1A2-B1+B2 | 0 |
| A1A2-B1B2+ | 0 |
| A1A2B1+B2+ | +2 |
| A1-A2-B1+B2 | -1 |
| A1-A2-B1B2+ | -1 |
| A1-A2B1+B2+ | +1 |
| A1A2-B1+B2+ | +1 |
| A1-A2-B1+B2+ | 0 |
Fig. 3 All microspecies with their charge values generated from the initial compound
Partition and distribution coefficients
Partition and distribution coefficients then can be expressed as follows:
- Partition coefficient of the neutral species is
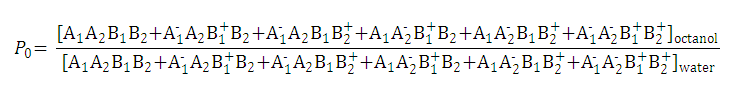
- Partition coefficients of the anionic and the cationic species are
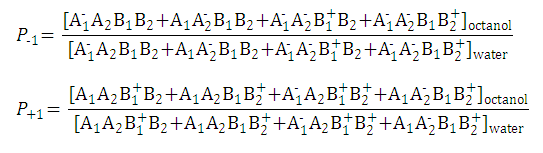
and
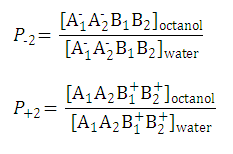
- Distribution coefficient of the original molecule is
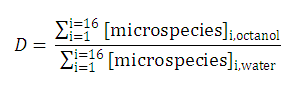
The micro partition coefficient is the ratio of the concentration of two microspecies defined with p i as expressed with the next relation:
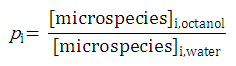
Relation between macro and micro partition coefficients
Macro partition coefficients P0…Pi can also be expressed as a function of micro partition coefficients p0…pi . From the definition of micro partition coefficients we obtain the following formula for the concentration of microspecies in octanol:
[microspecies] i,octanol = p i ⋅[microspecies] i,water
where p i is the micro partition coefficient of microspecies i .
For example, P -1 includes four micro partition coefficients ( p1, p2, p3, p4 ). They are given by the following formulae:
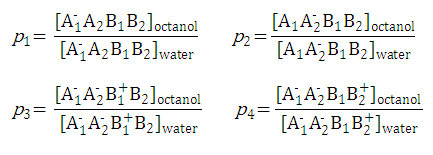
After substituting the p is into the original formula for P -1 we get the following simpler formula which includes only aqueous concentration of the appropriate microspecies:
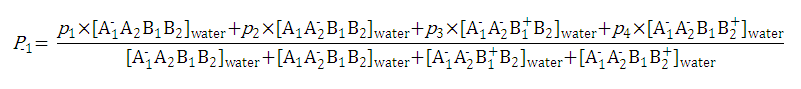
This can be further simplified if we introduce the acid dissociation constants of the A1A2B1B2 molecule. The next five ionization reactions of the A1A2B1B2 molecule are used to rearrange P -1 into a concentration free form:
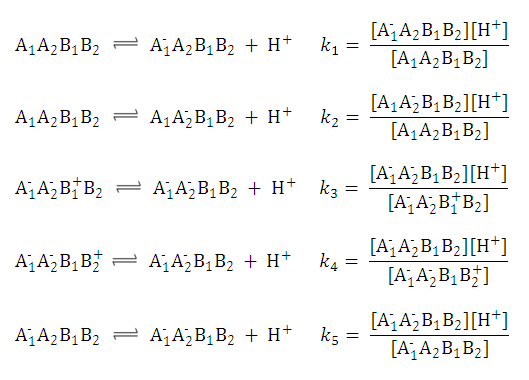
So we can further simplify the formula for P -1 to the following. This expression reveals that P -1 does not depend on the pH of the solution:
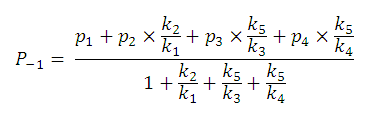
Similarly, one could show that P 0, P +1, P -2 and P +2 are also pH-independent.
In contrast to this, the distribution coefficient D does depend on the solution pH (see Klopman et al.):
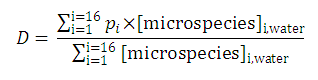
LogP calculation methods
Log P calculations are based on a pool of fragments predefined in the log P calculator. This set is based on the data set in Viswanadhan et al. Every fragment is assigned a unique name and a value. The log P value of a molecule is the sum of the fragment values that are present in the molecule.
{info} log P plugin handled only one fragment set until version 5.1.2, but then it was extended with two additional sets. The sets are based on a published data set (see Klopman et al.) and the PhysProp© database. These methods however are not available separately in the newer versions of the log P calculator.
The trainable log P calculation (available from version 5.1.3) offers the user to define his own log P database and calculate log P values based on experimental data. New fragment value extensions make a more precise calculation possible.
To have more information on the currently available log P calculation methods see this page.
Examples for logP and logD calculations
The following examples show log P /log D results for special molecules types. The calculations were performed with the default settings of the log P plugin.
Example #1
The compound below is zwitterionic that has the form of a A 1A 2B 1B 2 molecule mentioned in the theoretical section above. Lipophilicity of this compound reaches its maximum near to the isoelectric point. (pI is 4.43 in this case, while the global maximum of the log D function is 5.25. The calculated log D value at the pI point is 5.24.)
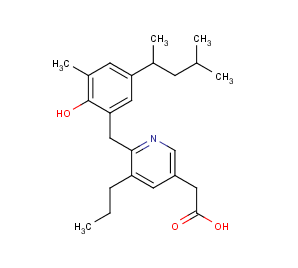
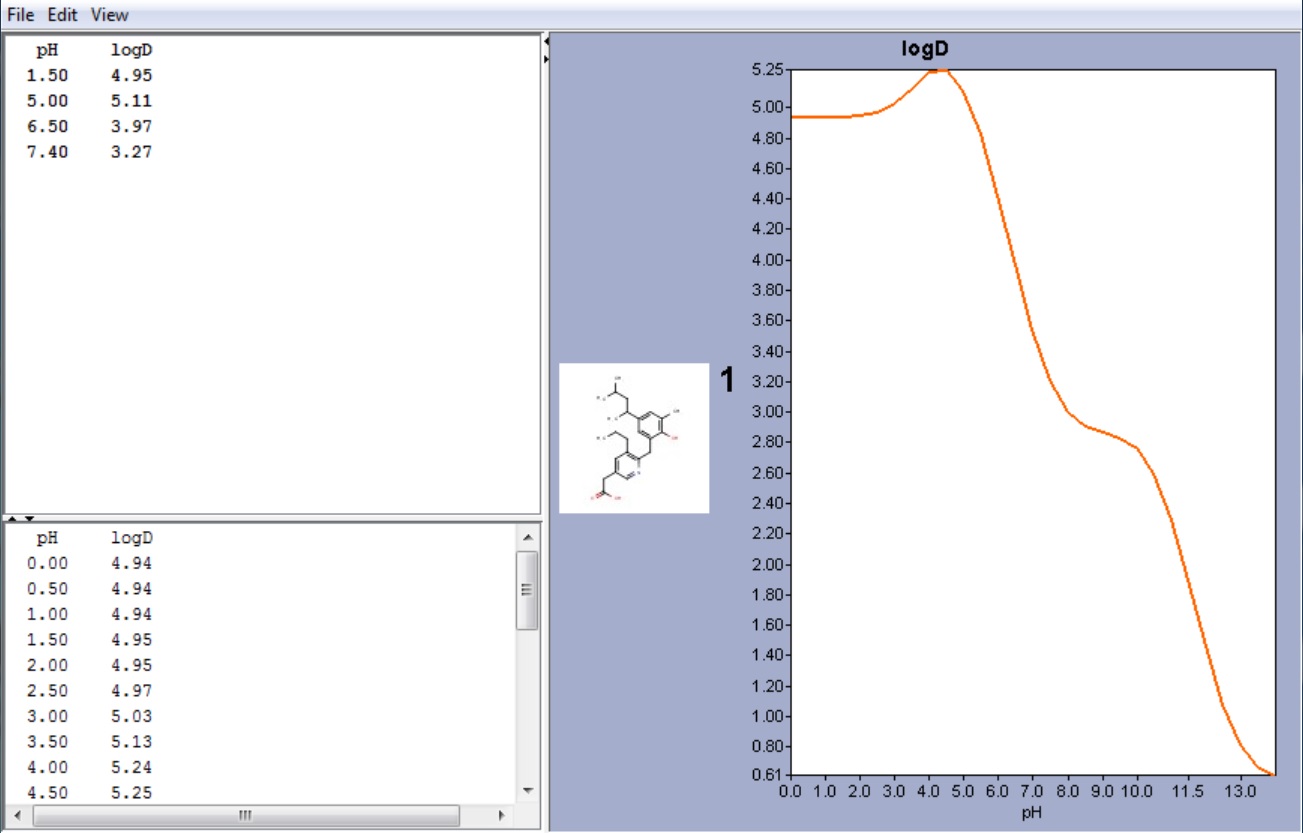
Fig. 3 Zwitterionic molecule and its lipophilicity plot
Example #2
Homidium is a quaternary ammonium ion with strong hydrophilic character. Its log P is calculated with the use of the ionic fragment of the N + ion. The calculated and measured log P values are -0.91 and -1.10, respectively .
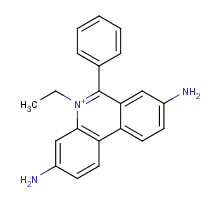
Example #3
Ibuprofen has the typical log D vs. pH profile that is characteristic of acidic compounds. Lipophilic behavior of ibuprofen will be dominant when its carboxylic group is unionized (at low pH). At higher pH values the carboxylic group reaches the fully ionized state and hydrofilicity becomes more enhanced.
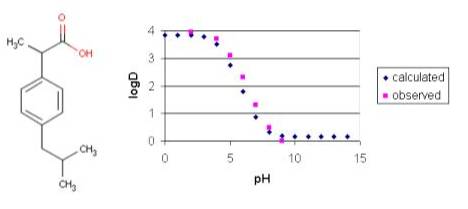
Fig. 6 Ibuprofen and its log D -pH plot
Example #4
The measured distribution coefficients also depends on the measurement method. The shake flask and the pH-metric methods are the most popular in practice. The figure below shows the calculated and measured log D of lignocaine as function of pH.
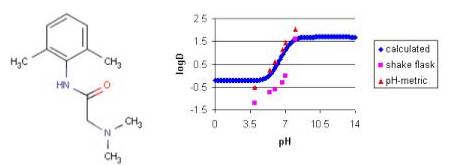
Fig. 7 Lignocaine and its logD-pHplot
References
-
Viswanadhan, V. N.; Ghose, A. K.; Revankar, G. R. and Robins, R. K., J.Chem.Inf.Comput.Sci. , 1989 , 29 , 3, 163-172; doi
-
Klopman, G.; Li, Ju-Yun.; Wang, S.; Dimayuga, M.: J.Chem.Inf.Comput.Sci. , 1994 , 34 , 752; doi
-
PhysProp© database, webpage
-
Csizmadia, F.; Tsantili-Kakoulidou, A.; Panderi, I. and Darvas, F., J.Pharm.Sci. , 1997 , 86 , 7, 865-871; doi
-
Bouchard, G.; Carrupt, P. A.; Testa, B.; Gobry, V. and Girault, H. H., Pharm.Res. , 2001 , 18 , 5, 702-708; doi